GG274 Homework 7: Summary Statistics, Histograms and Simulation

GG274 Homework 7: Summary Statistics, Histograms and Simulation#

Logistics#

Due date: The homework is due 23:59 on Monday, March 06.

You will submit your work on MarkUs. To submit your work:

Download this file (Homework_7.ipynb) from JupyterHub. (See our JupyterHub Guide for detailed instructions.)
Submit this file to MarkUs under the hw7 assignment. (See our MarkUs Guide for detailed instructions.) All homeworks will take place in a Jupyter notebook (like this one). When you are done, you will download this notebook and submit it to MarkUs.

Piloting MarkUs JupyterHub Extension (optional)#

Starting with this week’s lab and homework, we’re piloting a new way to submit files to MarkUs directly from JupyterHub (without needing to download them). This is optional so you can still submit your work the usual way, but if you have some time please try it out by following the instructions on the MarkUs Guide.

Introduction#

For this week’s homework, we’ll investigate the behaviour of sample statistics and distributions as we vary our sample size. Specifically, we’ll be investigating the mean amount of time spent cleaning by respondents. Furthermore, we will extend our analysis by studying how our sample mean estimate tends to change when we take samples of increasing sizes.

Question#

Question: How much time on average do respondents spend on indoor house cleaning? How does our estimate of a sample mean change as we take increasingly larger samples?

Instructions and Learning Objectives#

In this homework, you will:

Work with the Time Use dataset from lecture to investigate properties of sampling means as the sample size changes
Create and modify for loops and functions to run sampling simulations
Visualize data using histograms and scatter plots

Task 1 - Read in data#

The Data part of your notebook should read the raw data, extract a DataFrame containing the important columns, rename the columns, and filter out missing values.

You might find it helpful to name intermediate values in your algorithms. That way you can examine them to make sure they have the type you expect and that they look like what you expect. Very helpful when debugging!

Step 1#

Create the following pandas DataFrames:

time_use_data_raw: the DataFrame created by reading the gss_tu2016_main_file.csv file. (1 mark)
time_use_dur: the DataFrame containing the following columns from time_use_data_raw: 'CASEID', 'dur18'. (1 mark) (We test this after any changes are made to it. We do not check the initial value.)

# Sample solution, delete to create handout
import pandas as pd
import matplotlib.pyplot as plt

time_use_data_raw = pd.read_csv('gss_tu2016_main_file.csv')

time_use_dur = time_use_data_raw[["CASEID",
                                   "dur18"]]

/var/folders/0j/ybsv4ncn5w50v40vdh5jjlww0000gn/T/ipykernel_99251/207783302.py:2: DeprecationWarning: 
Pyarrow will become a required dependency of pandas in the next major release of pandas (pandas 3.0),
(to allow more performant data types, such as the Arrow string type, and better interoperability with other libraries)
but was not found to be installed on your system.
If this would cause problems for you,
please provide us feedback at https://github.com/pandas-dev/pandas/issues/54466
        
  import pandas as pd

Step 2#

time_use_dur could use more informative column names.

Replace CASEID and dur18 in time_use_dur by

creating a dictionary new_column_names that maps the column names from time_use_dur to the values 'participant_id' and 'time_spent_cleaning'. (1 mark)
create a new DataFrame stored in time_use_data that is a copy of time_use_dur, but with the columns renamed using new_column_names. (1 mark)

# Sample solution, delete to create handout
new_column_names = {
    "CASEID": "participant_id",
    "dur18": "time_spent_cleaning",
}

time_use_data = time_use_dur.copy()

time_use_data.rename(columns=new_column_names, inplace=True)

time_use_data

	participant_id	time_spent_cleaning
0	10000	0
1	10001	0
2	10002	120
3	10003	0
4	10004	0
...	...	...
17385	27385	0
17386	27386	0
17387	27387	30
17388	27388	10
17389	27389	135

17390 rows × 2 columns

# Step 2 check that you have the correct column names
# leave this for students to check work

expected_columnnames = ['participant_id', 'time_spent_cleaning']

try:
    assert expected_columnnames == list(time_use_data.columns)
    print('Column names are correct!')
except:
    print('Something is wrong, check your column names')

Column names are correct!

Task 2 - Compute and Visualize Distribution#

Step 1#

Compute the distribution of the column time_spent_cleaning for respondents that spent at least some time cleaning (i.e., had a non-zero value of time_spent_cleaning) in time_use_data using the describe function. To do this

Create a pandas Series called clean_nonzero that only has respondents with non-zero values of time_spent_cleaning.
Use the describe function to describe the distribution of time_spent_cleaning, and store the results in a variable called summary_stats.

# Sample solution, delete to create handout
clean_nonzero = time_use_data[time_use_data["time_spent_cleaning"] > 0]['time_spent_cleaning']

summary_stats = clean_nonzero.describe()

summary_stats

count    7154.000000
mean       91.095192
std        94.963051
min         5.000000
25%        30.000000
50%        60.000000
75%       120.000000
max       855.000000
Name: time_spent_cleaning, dtype: float64

Step 2#

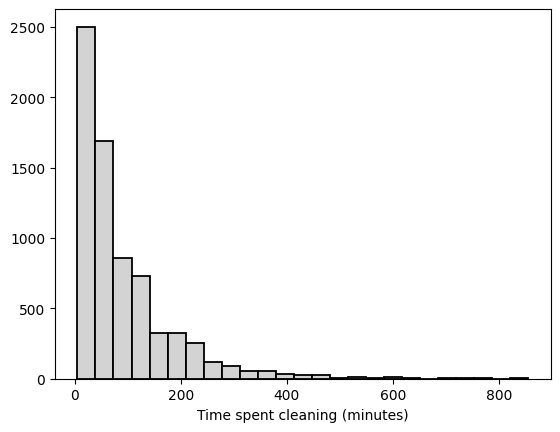
Visualize clean_nonzero column by creating a histogram using maptplotlib with the following parameters:

bins = 25, edgecolor='black', linewidth = 1.3, color = 'lightgrey'

Label the horizontal axis (x-axis) Time spent cleaning (minutes).

# Sample solution, delete to create handout
plt.hist(clean_nonzero, bins=25, edgecolor='black', linewidth = 1.3, color = 'lightgrey')

plt.xlabel('Time spent cleaning (minutes)')

Text(0.5, 0, 'Time spent cleaning (minutes)')

../../../../_images/63b167c0044f3e6bc18ade60bb897d6b9755528c3891e7f8a14f4b54edbb6ce3.png

Step 3#

In a markdown cell, describe the distribution of data, pointing out features like mode (where most observations lie), skew, and potential outliers. Do our results make sense given what we know about time spent on daily cleaning?

Are there any strange values? Specifically, does it make sense for people to spend 0 mins cleaning? Briefly explain. (2 marks)

From the histogram, you can tell that the data is right-skewed (or a decreasing shape; you don’t need to use the exact term), ranges between 0 and just above 800, centred around the lower end (0~200), etc. There is a large number of values with 0 minute. One may argue that it doesn’t make sense to have so many people spend 0 minute cleaning in a day or argue the other way. e.g., perhaps it’s reasonable to assume people clean as they are involved in other activities but don’t recognize it as time spent on cleaning. Any reasonable explanation based on the context would be acceptable.

Task 3: Compute the empirical mean#

The empirical mean as the mean of all observed data. We distinguish this from the sample mean which is the mean of a sample or portion of all data.

Compute the empirical mean time spent cleaning by respondents and name it empirical_mean_time_spent_cleaning. (1 mark)

# Sample solution, delete to create handout
empirical_mean_time_spent_cleaning = clean_nonzero.mean()

empirical_mean_time_spent_cleaning

91.09519150125804

Task 4: Set up a Simulation Experiment#

You will investigate the behaviour of sample means for the following sample sizes:

5, 10, 20, 50, 100, 200, 500, and 1000.

Step 1 - Specify Sample Sizes#

Create a list named sample_sizes with the aforementioned values in the specified order. (1 mark)

# Sample solution, delete to create handout
sample_sizes = [5, 10, 20, 50, 100, 200, 500, 1000]

Step 2 - Simulating Sample Means#

In this part, you will complete a function that creates and returns a list of the sample means of the sample draws.

Name the function simulate_sample_means.

The function will have two arguments:

data: a pandas Series or column of a DataFrame that we are sampling
N: an int, the size of the sample we draw

Your function should make and return a list of 100 sample means of size N from data.

Sample without replacement.

The function will return a list, sample_means. The list will be of size 100, with each element in the list representing the sample mean from the sample of size N. Hint: Initialize an empty list used to store the sample means. Inside your for loop generate a sample from the data, calculate the sample mean, and append it to your list.

Wherever there is a commented chunk of code of the form var_name = ..., replace the ... with the appropriate value or expression.

# Sample solution, delete to create handout

def simulate_sample_means(data, N):
    '''Return a list of 100 sample means from a sample of size N from data.'''
    
    # This next statement is for reproducability: each random number is generated
    # mathematically based on the previous random number, and we can say which
    # number to start with when we call sample. This allows us to have reproducability
    # with "random" numbers and so we can autotest! Yay!
    seed = 0

    # Create any variables you need here, such as the list of sample means you are
    # accumulating.
    sample_means = []
    
    # generate a sample of size N and compute sample mean.
    # append the sample mean to the list of sample means.
    # repeat 100 times.
    
    for _ in range(100):
        seed += 1 # Don't change this line
        
        # Here, write code to:
        # 1) Take a sample of data, and calculate the sample mean.
        #    When you call .sample, make sure you use random_state=seed as one of the
        #    arguments.
        # 2) Append the sample mean to the list of sample means.
        sample_mean = data.sample(N, replace=False, random_state=seed).mean()
        
        sample_means.append(sample_mean)
        
    return sample_means

simulate_sample_means(clean_nonzero, 5)

[112.0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0]

# Uncomment to create handout

# # Finish the function header and complete the function body.
# # 
# def 

#     '''Return a list of 100 sample means from a sample of size N from data.'''
#     
#     

#     # This next statement is for reproducability: each random number is generated
#     # mathematically based on the previous random number, and we can say which
#     # number to start with when we call sample. This allows us to have reproducability
#     # with "random" numbers and so we can autotest! Yay!
#     seed = 0

#     # Create any variables you need here, such as the list of sample means you are
#     # accumulating.

    
#     # generate a sample of size N and compute sample mean.
      # append the sample mean to the list of sample means.
      # repeat 100 times.

#     for _ in range(100):
#         seed += 1 # Don't change this line
        
#         
#         # Here, write code to:
#         # 1) Take a sample of data, and calculate the sample mean.
#         #    When you call .sample, make sure you use random_state=seed as one of the
#         #    arguments.
#         # 2) Append the sample mean to the list of sample means.
#         
#         
#          
#     return ???

Task 5 - Simulate Sample Means#

In this part, you will complete a code block that computes and compiles simulated means for each sample size.

For each sample size in sample_sizes, call function simulate_sample_means from the previous step to calculate 100 sample means at that sample size. You’re going to build a dictionary where each key is a sample size and each value is the corresponding list of means that simulate_sample_means returned.

Accumulating information in a dictionary#

Remember in lecture we used a for loop to add up a series of numbers? And then we used a for loop to accumulate a list of means? As it turns out, you can use the same technique to make a dictionary.

Here’s how you add a key/value pair to a dictionary (this is also called “inserting”):

d = {}
d['key1'] = 'value1'
d

{'key1': 'value1'}

d['key2'] = 'value2'
d

{'key1': 'value1', 'key2': 'value2'}

d['key1'] = 'new_value'
d

{'key1': 'new_value', 'key2': 'value2'}

You can accumulate a new dictionary using a for loop:

ta_to_course = {}
for name in ['Amber','Martin', 'Davia', 'KP', 'Ilan']:
    ta_to_course[name] = 'GGR274'

ta_to_course

{'Amber': 'GGR274',
 'Martin': 'GGR274',
 'Davia': 'GGR274',
 'KP': 'GGR274',
 'Ilan': 'GGR274'}

for name in ['Matt', 'Fiona']:
    ta_to_course[name] = 'EEB125'

print(ta_to_course)
print(ta_to_course['Matt'])

{'Amber': 'GGR274', 'Martin': 'GGR274', 'Davia': 'GGR274', 'KP': 'GGR274', 'Ilan': 'GGR274', 'Matt': 'EEB125', 'Fiona': 'EEB125'}
EEB125

Step 1 - Create a dictionary of simulated means for each sample size#

As you loop through each element in sample_sizes, you will pass the current sample size to the function simulate_sample_means (specifically, the argument N). You will be sampling from the cleaned dataset, so make sure to pass the value of clean_nonzero to the data parameter.

The result of calling simulate_sample_means is a list of means. Add a new key/value pair to all_sample_means_by_sample_size. The key is the current sample size and the value is the list of means.

Finally we will be checking this in the autotester:

all_sample_means_by_sample_size: a dictionary mapping the sample sizes to a list of sample means of a size 100. (Because we’ll use the same random seed, we’ll get the same “random” sequence. That means that we can autotest it. Yay!) (2 marks)

# Sample solution, delete to create handout

all_sample_means_by_sample_size = {}

for sample_size in sample_sizes:
        
    mean_at_sample_mean = simulate_sample_means(data = clean_nonzero, N = sample_size)
        
    all_sample_means_by_sample_size[sample_size] = mean_at_sample_mean

# Uncomment to create handout
# feel free to add more starter code if you feel it's appropriate

# # Finish the code

# # 
# all_sample_means_by_sample_size_as_dict = {}

# for 

Step 2 - Answer this question#

Briefly explain what the keys and values represent in the dictionary all_sample_means_by_sample_size. You can obtain the keys by using the keys method all_sample_means_by_sample_size.keys().

print(all_sample_means_by_sample_size.keys())
print(all_sample_means_by_sample_size.values())

dict_keys([5, 10, 20, 50, 100, 200, 500, 1000])
dict_values([[112.0, 70.0, 155.0, 43.0, 102.0, 63.0, 76.0, 92.0, 83.0, 103.0, 99.0, 53.0, 78.0, 60.0, 70.0, 48.0, 128.0, 225.0, 74.0, 53.0, 59.0, 69.0, 46.0, 149.0, 200.0, 69.0, 45.0, 40.0, 114.0, 47.0, 43.0, 177.0, 149.0, 42.0, 140.0, 55.0, 70.0, 54.0, 84.0, 106.0, 85.0, 67.0, 152.0, 65.0, 77.0, 85.0, 104.0, 155.0, 59.0, 46.0, 124.0, 103.0, 46.0, 67.0, 70.0, 106.0, 255.0, 66.0, 159.0, 159.0, 92.0, 74.0, 87.0, 45.0, 84.0, 78.0, 78.0, 157.0, 46.0, 52.0, 113.0, 120.0, 86.0, 137.0, 49.0, 27.0, 123.0, 32.0, 47.0, 93.0, 159.0, 26.0, 94.0, 155.0, 82.0, 145.0, 69.0, 117.0, 51.0, 33.0, 54.0, 77.0, 67.0, 51.0, 68.0, 50.0, 160.0, 139.0, 62.0, 108.0], [74.0, 74.0, 129.5, 52.5, 123.5, 97.0, 72.0, 104.5, 95.5, 99.0, 99.5, 60.0, 68.0, 47.0, 74.5, 78.5, 98.5, 165.5, 71.0, 65.5, 67.5, 77.0, 111.5, 128.0, 130.0, 81.5, 83.5, 71.5, 82.0, 72.0, 69.5, 135.0, 106.0, 104.0, 112.0, 77.5, 64.5, 70.0, 79.0, 84.0, 106.0, 74.5, 109.5, 72.0, 88.5, 63.5, 104.5, 150.0, 62.5, 70.5, 104.5, 78.0, 73.0, 60.5, 62.0, 105.5, 197.5, 78.5, 138.5, 128.5, 87.5, 74.0, 77.5, 57.5, 100.5, 106.5, 88.0, 105.5, 72.5, 96.5, 93.5, 101.0, 65.5, 106.5, 92.0, 57.0, 92.5, 34.5, 90.5, 73.0, 109.0, 56.5, 59.0, 116.5, 90.5, 100.5, 73.0, 121.0, 137.0, 47.0, 87.5, 67.5, 72.0, 44.0, 106.0, 58.0, 125.5, 127.5, 72.4, 82.5], [55.75, 69.25, 89.25, 70.0, 106.75, 78.75, 67.0, 103.25, 82.5, 84.75, 76.0, 72.0, 96.5, 72.25, 86.25, 93.5, 78.25, 114.75, 79.5, 80.0, 72.25, 82.5, 90.5, 115.25, 97.0, 102.5, 68.75, 76.5, 87.75, 95.75, 73.0, 109.5, 127.25, 129.5, 124.5, 75.5, 79.0, 80.5, 79.25, 96.75, 98.0, 99.25, 87.0, 112.25, 74.0, 89.75, 87.0, 122.0, 69.25, 49.5, 101.25, 89.5, 77.0, 68.25, 65.25, 86.25, 145.25, 77.0, 98.0, 119.5, 89.75, 81.25, 80.75, 86.0, 78.75, 96.5, 110.0, 89.75, 79.75, 88.0, 95.25, 78.75, 67.25, 87.0, 75.25, 66.0, 110.0, 46.25, 105.5, 81.0, 106.5, 70.25, 89.5, 110.75, 76.25, 101.5, 75.0, 117.25, 140.5, 60.5, 91.5, 89.0, 69.0, 67.75, 112.25, 105.5, 101.5, 112.0, 81.95, 95.0], [79.6, 76.3, 104.9, 86.6, 100.5, 90.2, 98.2, 99.7, 87.3, 76.0, 72.1, 67.0, 86.0, 62.4, 114.7, 96.8, 91.1, 115.6, 91.3, 94.0, 90.9, 104.7, 74.4, 106.2, 87.8, 82.8, 92.6, 73.6, 100.2, 90.6, 74.9, 106.72, 103.3, 118.8, 110.8, 84.3, 97.4, 107.6, 96.9, 83.5, 86.3, 109.6, 71.9, 84.2, 88.7, 106.0, 85.2, 103.4, 93.1, 74.8, 92.2, 97.1, 85.8, 75.5, 107.8, 88.9, 140.7, 90.6, 83.6, 97.9, 76.4, 102.3, 91.1, 98.8, 98.4, 79.6, 102.4, 73.9, 118.1, 110.2, 91.9, 94.9, 100.6, 94.2, 81.1, 76.1, 108.0, 61.2, 84.3, 93.5, 101.9, 87.7, 104.4, 91.5, 71.1, 85.3, 90.2, 99.9, 109.7, 60.2, 88.6, 108.0, 72.3, 78.8, 103.8, 106.9, 84.6, 90.4, 86.98, 139.5], [76.5, 78.35, 89.9, 93.65, 91.5, 94.45, 94.6, 90.55, 88.3, 68.0, 72.8, 73.5, 95.4, 70.75, 105.4, 86.45, 97.05, 102.05, 93.7, 93.5, 97.7, 99.45, 86.55, 100.25, 99.5, 85.6, 81.45, 82.75, 97.9, 89.25, 83.05, 86.36, 93.5, 103.4, 99.55, 95.75, 101.1, 109.2, 94.4, 77.45, 87.7, 95.5, 74.55, 82.75, 87.35, 105.54, 89.05, 89.95, 89.8, 81.05, 97.25, 85.85, 89.8, 80.6, 93.25, 86.15, 113.0, 89.0, 87.35, 88.55, 96.35, 103.1, 84.65, 98.6, 89.5, 77.0, 89.6, 83.75, 105.75, 94.3, 89.65, 91.05, 96.05, 87.25, 83.6, 93.5, 89.95, 74.95, 82.4, 85.75, 97.8, 93.65, 90.65, 84.85, 78.95, 81.55, 94.15, 95.9, 92.1, 82.55, 95.15, 104.5, 82.5, 86.25, 106.4, 95.5, 96.75, 98.1, 97.74, 110.4], [80.65, 73.475, 96.15, 94.325, 89.25, 100.0, 91.15, 85.35, 84.25, 86.075, 85.875, 86.225, 84.025, 89.175, 93.025, 91.625, 100.35, 99.35, 92.95, 89.675, 86.575, 91.375, 94.55, 99.325, 89.125, 88.1, 86.325, 87.77, 96.6, 84.8, 84.75, 82.53, 96.5, 95.975, 94.6, 97.4, 97.9, 96.425, 89.25, 81.575, 86.975, 92.125, 71.2, 88.4, 92.2, 101.42, 90.925, 92.125, 94.05, 89.55, 99.8, 88.3, 87.65, 87.05, 91.475, 95.6, 106.825, 94.72, 86.825, 91.645, 88.075, 96.275, 88.35, 96.425, 82.55, 80.8, 90.37, 93.475, 93.0, 87.85, 84.65, 96.425, 93.6, 97.75, 88.2, 97.3, 87.975, 83.7, 85.45, 83.175, 87.675, 99.575, 80.75, 90.925, 92.85, 87.4, 98.375, 96.3, 106.775, 83.025, 90.2, 94.975, 94.375, 98.675, 96.225, 91.125, 94.65, 96.275, 96.195, 99.5], [85.49, 80.82, 91.79, 94.59, 86.88, 91.86, 85.45, 91.062, 92.76, 92.79, 88.28, 89.762, 85.53, 92.2, 92.27, 91.008, 96.7, 89.43, 91.45, 86.602, 91.43, 93.34, 93.39, 93.08, 94.46, 92.1, 90.032, 90.678, 98.39, 83.59, 90.45, 88.082, 96.12, 93.942, 92.448, 90.23, 96.448, 99.948, 90.5, 87.03, 89.69, 90.81, 79.498, 85.14, 95.9, 94.488, 88.93, 96.412, 95.502, 90.64, 92.14, 89.37, 91.042, 89.74, 88.452, 91.43, 100.52, 95.738, 85.03, 93.238, 98.55, 93.38, 84.66, 97.43, 86.26, 88.71, 90.028, 92.99, 92.48, 92.238, 86.34, 90.77, 97.74, 89.28, 87.18, 87.22, 88.61, 87.76, 92.55, 87.46, 89.54, 90.53, 87.138, 91.852, 91.158, 87.29, 92.62, 101.03, 98.66, 90.58, 96.76, 91.68, 89.042, 94.86, 101.17, 94.0, 93.25, 94.66, 90.798, 97.11], [90.374, 90.405, 93.855, 95.23, 93.335, 89.36, 89.035, 92.305, 94.074, 94.24, 86.465, 89.836, 89.375, 89.34, 92.92, 89.004, 93.295, 90.97, 93.74, 91.286, 89.34, 93.235, 91.82, 96.275, 94.991, 88.179, 88.296, 93.835, 94.72, 86.45, 91.811, 84.876, 91.27, 94.831, 90.37, 91.095, 95.344, 93.229, 91.46, 91.715, 88.82, 95.02, 85.164, 86.7, 92.1, 91.069, 93.65, 92.026, 89.35, 91.18, 94.96, 92.041, 92.171, 90.27, 87.531, 90.004, 93.23, 95.17, 88.22, 93.721, 95.37, 91.321, 87.845, 95.335, 89.125, 90.35, 90.194, 90.271, 93.641, 93.219, 90.245, 94.16, 93.82, 86.625, 88.89, 89.16, 88.415, 85.72, 93.514, 89.244, 88.659, 94.689, 89.23, 92.691, 92.129, 90.34, 92.26, 94.81, 95.67, 90.03, 92.431, 88.57, 90.94, 90.555, 99.355, 92.245, 90.891, 94.78, 91.219, 93.94]])

The keys in the dictionary represent the sample size used to simulate the values. Note that the keys have 8 numbers and values have 8 list of 100 simulated values using the sample sizes in the corresponding keys.)

Task 6 - Plot the results#

Step 1: Create Data for Plotting#

In this section you will calculate the mean of simulation.

Create the following variables:

sample_means_by_sample_size: a DataFrame created from the dictionary all_sample_means_by_sample_size. (1 mark)
mean_of_sample_means_by_sample_size: compute the column means of sample_means_by_sample_size, that is the mean sample means at each sample size. (1 mark)
diff_sample_mean_empirical_means_by_sample_size: the difference between mean of sample means and the empirical mean at each sample size. (1 mark)

sample_means_by_sample_size = pd.DataFrame(all_sample_means_by_sample_size)

mean_of_sample_means_by_sample_size = sample_means_by_sample_size.mean()

diff_sample_mean_empirical_means_by_sample_size = mean_of_sample_means_by_sample_size - empirical_mean_time_spent_cleaning

mean_of_sample_means_by_sample_size

     89.82000
    89.08400
    89.01200
    92.40400
   90.76790
   91.14500
   91.41486
  91.45881
dtype: float64

Step 2: Plot the data#

In this section you will plot the results.

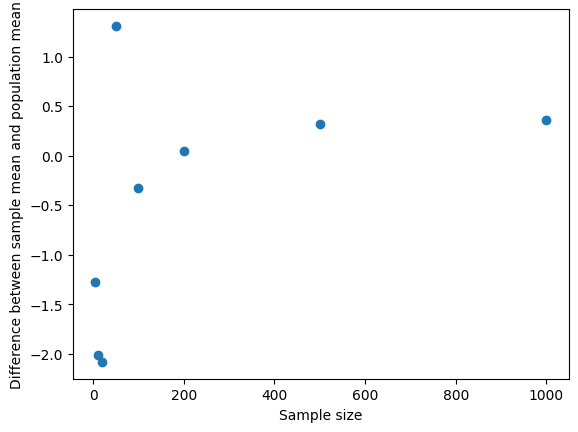
Create a scatter plot using matplotlib with

diff_sample_mean_empirical_means_by_sample_size.index on the horizontal axis (x-axis) and
diff_sample_mean_empirical_means_by_sample_size on the vertical axis (y-axis).

Label the horizontal axis with the text Sample size and the vertical axis with the text Difference between sample mean and population mean.

plt.scatter(diff_sample_mean_empirical_means_by_sample_size.index, diff_sample_mean_empirical_means_by_sample_size)

plt.xlabel('Sample size')

plt.ylabel('Difference between sample mean and population mean')

Text(0, 0.5, 'Difference between sample mean and population mean')

../../../../_images/e0b4dc3ae9fc4ad2d5cd915ab34d368fcc957776752b922c0ccea973b957d992.png

Task 7 - Answer the following Questions#

Include cells with your answers to each of these questions:

What is the empirical mean time spent cleaning by respondents per day (in minutes). Does this value make sense? Why or why not? Answer in one line. (1 mark)

The empirical mean time spent cleaning is stored in empirical_mean_time_spent_cleaning. It is approximately 91 minutes. It seems reasonable that people spend about an hour and a half cleaning per day on average. (Any reasonable argument based on the context and the correctvalue is acceptable.)

Based on your final scatter plot, what trend or pattern do you notice between sample size and difference between the mean of sample means and empirical mean? Does the difference decrease or increase with sample size? Explain why this trend is seen, drawing on your understanding of randomness of sampling. (2 marks)

As the sample size increases, the difference becomes closer to 0. This is due to the law of averages (or explain that with a larger sample size, a random sample is more likely to represent the population closesly.)

If you were to do further analysis to study how the time spent cleaning is different for various subpopulations, which additional sociodemographic variables might you consider? Why? Write 3-5 sentences identifying 1-2 variables (e.g. age - don’t pick this!) of interest and what differences in cleaning time you might expect to find.

(Any sociodemographic variable is acceptable with a reasonable expected difference identified.)

GG274 Homework 7: Summary Statistics, Histograms and Simulation

Contents

GG274 Homework 7: Summary Statistics, Histograms and Simulation#

Logistics#

Piloting MarkUs JupyterHub Extension (optional)#

Introduction#

Question#

Instructions and Learning Objectives#

Task 1 - Read in data#

Step 1#

Step 2#

Task 2 - Compute and Visualize Distribution#

Step 1#

Step 2#

Step 3#

Task 3: Compute the empirical mean#

Task 4: Set up a Simulation Experiment#

Step 1 - Specify Sample Sizes#

Step 2 - Simulating Sample Means#

Task 5 - Simulate Sample Means#

Accumulating information in a dictionary#

Step 1 - Create a dictionary of simulated means for each sample size#

Step 2 - Answer this question#

Task 6 - Plot the results#

Step 1: Create Data for Plotting#

Step 2: Plot the data#

Task 7 - Answer the following Questions#